Basit makineler ünitesine dişliler kasnaklar ve çıkrık ile devam edip konu anlatımı yapıp örnek sorular çözeceğiz.
A.Dişliler
Üzerinde eşit aralıkla yerleştirilmiş dişler bulunan ve belirli bir eksen etrafında dönebilen disk şeklindeki araçlardır.
İş makineleri, otomobiller ve matkaplar gibi birçok farklı yerde kullanılırlar. Dönme hızının veya yönünün değişmesini istediğimiz durumlarda kullanılır.
Dişlilerden biri saat yönünde dönerken diğeri saat yönünün tersi yönde döner. Yani dişliler yan yana yerleştirildiklerinde birbirlerini zıt yönde döndürürler. Çarkların dişli sayıları eşit değilse diş sayısı fazla olan çark daha az döner. Çarkların diş sayısı arttıkça dönme sayısı ve dönüş hızı azalır. Çarkların diş sayısı aynı ise zıt yönde ve aynı sayıda dönerler.
Tur sayısı için formül =n1.r1=n2.r2
n1=1.dişlinin attığı tur sayısı
r1=1. dişlinin yarı çapı
n2=2. dişlinin attığı tur sayısı
r2=2. dişlinin attığı tur sayısı
Öğretmen notu = Bu formül hem dişliler hemde kasnaklar için geçerlidir. Dişlilerle ve kasnaklarla ilgili soruları çözerken formül işimizi kolaylaştırıyor fakat dişliler arasında tur sayısının yarı çapla ters orantılı olduğunu bilerek soruları çözmek sizi formül ezberleme durumundan kurtarır.

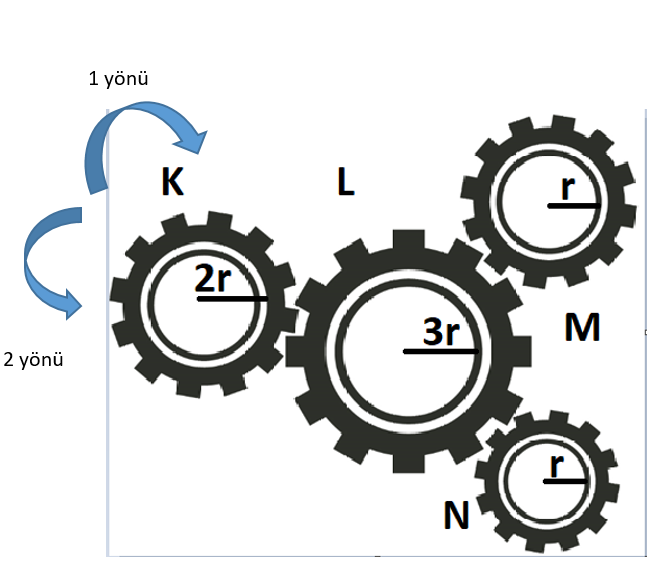
Örnek :Şekil-2 de K dişlisi 1 yönünde 6 tur döndüğüne göre L, M, N dişlileri hangi yönde kaç tur atar ?
K dişlisi 1 yönünde dönüyorsa, L dişlisi 2 yönüne döner. L dişlisine bağlı dönen M ve N dişlisi, L dişlisinin ters yönünde dönecekler. O halde M ve N dişlisi 1 yönünde dönmeye başlar.
Tur sayılarını bulmak için :
Formülsüz çözüm :
K dişlisinin 2r yarıçapı vardır ve 6 tur dönmektedir. L dişlisi 3r yarıçapına sahiptir. L dişlisi, K dişlisinden yarıçap olarak büyük olduğu için daha az sayıda tur atacaktır.
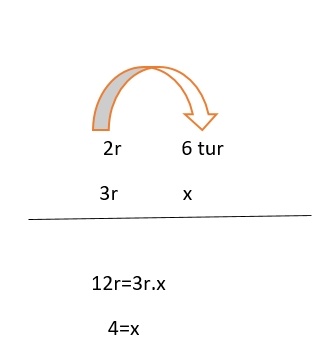
Çözüm yaparken ters orantıyı kullanmalıyız. Tur sayısı ve yarıçap yan yana çarpılarak bulunur. 3r büyük yarıçaplı L dişlisi daha az döndüğünü bulmak işlemin doğru olduğunu gösterir.
Şimdi L dişlisine bağlı dönen M ve N dişlileri için işlem yapalım.
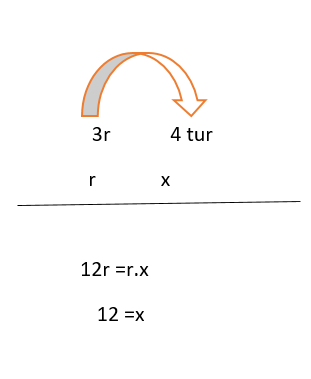
M ve N dişlisi r yarı çapına sahip iki dişlidir. L dişlisine göre 3 kat daha küçük yarı çaplara sahip iki dişli, L dişlisinin attığı tur sayısından 3 kat fazla olmuştur.
B. Kasnaklar
Bir merkez etrafında dönebilen silindir şeklindeki cisimlere denir. Birbirlerine kayış ya da zincirle bağlıdırlar.
Eğer kayış düz bağlanmışsa aynı yönde dönerler.
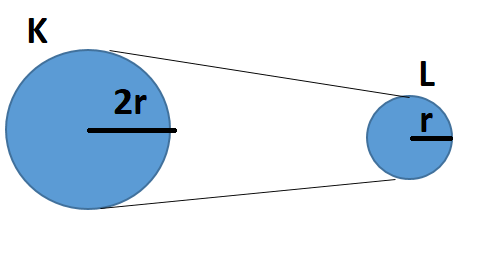
K ve L kasnağı birbiri ile düz bir kayışla bağlanmışlardır. K saat yönünde dönerse L de saat yönünde dönmeye başlar.
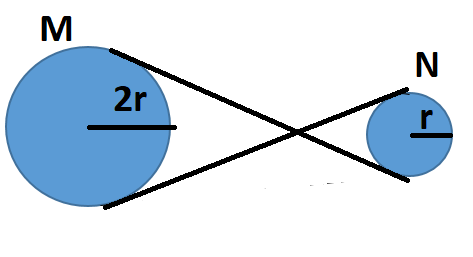
M ve N kasnağı birbiri ile zıt olarak bağlanmıştır. Birbirlerine zıt yönde dönemeye başlayacaktır. O halde M kasnağı saat yönünde dönmeye başlarsa N kasnağı saat yönünün tersine dönecektir.
Şimdi sizinle M ve N kasnaklarının tur sayılarını yorumlayalım. Dişliler ile aynı durum söz konusu yarıçapları oranında tur sayıları büyük olanın daha az tur sayısı atması, küçük olanın ise daha çok tur atması söz konusudur.
M kasnağı 2r yarıçapı ile 6 tur döners , ondan daha küçük olan N kasnağı r yarıçapı ile ona yetişmek için 12 tur atması gerekecektir.
Çakışık merkezli Dişli ve Kasnaklar
Farklı yarı çaplarda aynı merkez etrafında dönen dişli ve kasnaklardır. Aynı merkez etrafında dönemleri hem aynı yöne dönmelerini hem de aynı turda dönmelerini sağlar.

Hem kasnaklar hem de dişliler şekilde görüldüğü gibi bir merkez etrafında dönmektedirler. Bu durumda yarı çaplarına bakmamıza gerek kalmaksızın aynı yönde aynı turu atıklarını söyleyebiliriz. R kasnağı saat yönüne doğru 2 tur atıyorsa P kasnağı saat yönünde 2 tur atar. L dişlisi saat yönünde 5 tur atıyorsa K dişlisi saat yönünde 5 tur atar.
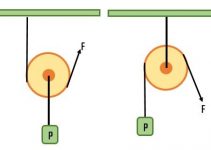
C. Çıkrık
Aynı eksen etrafından dönen farklı yarı çaplardaki silindire Çıkrık denir.
Kuyudan su çekmek için, kahve değirmenlerinde, bisiklet pedalında , tornavida, araba anahtarları ve araba direksiyonlarında çıkrık karşımıza çıkar.

Tornavida iki farklı yarı çaplı silindirin bir araya gelmesi ile oluşur. Bu iki silindirin dönmesi ile çıkrık meydana gelir.
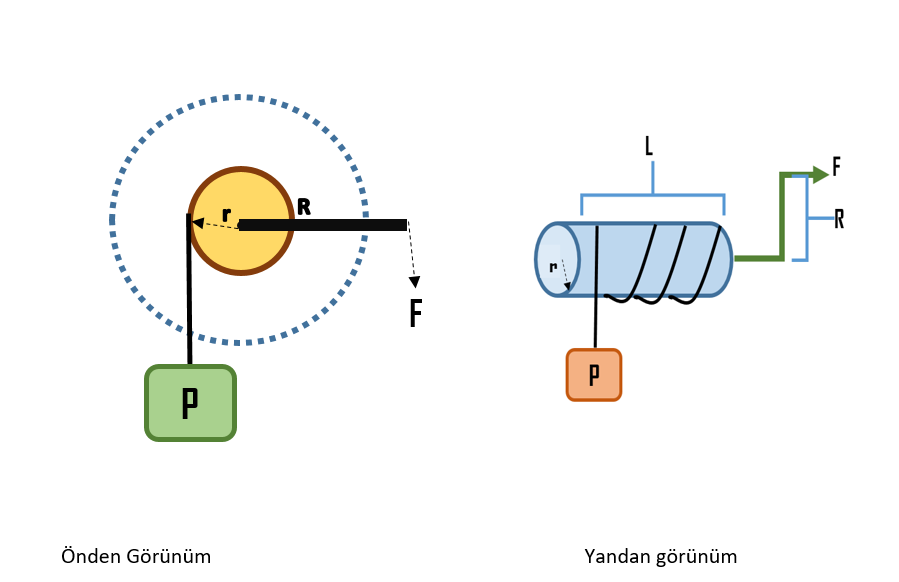
P=Yük
F=Kuvvet
r =Yük yolu
R=Kuvvet yolu
Çıkrıkta işlem ve kuvvet kazancı yorumları yapmak aynı kaldıraçtaki gibidir. Kuvvet yolu R’nin büyümesi kuvvet kazancını arttırır yoldan kayıp meydana gelir. Yani kuvvet küçük olur. Yük yolu r’nin büyümesi ise kuvvetin artmasına sebep olur.
Kaldıraçtaki formülü hatırlayalım :
Kuvvet x Kuvvet yolu=Yük x Yük yolu
Aynı durumu çıkrık için uyarlayalım :
FXR=Pxr Kodlaması =Pire FaRe 🙂
Dişliler kasnaklar ve çıkrık çalışma kağıdına buradan ulaşabilirsiniz.
Güncel konular için facebook , instagram ve google+ üzerinden bizi takip edebilirsiniz. Tekrar görüşmek üzere.